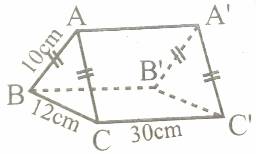
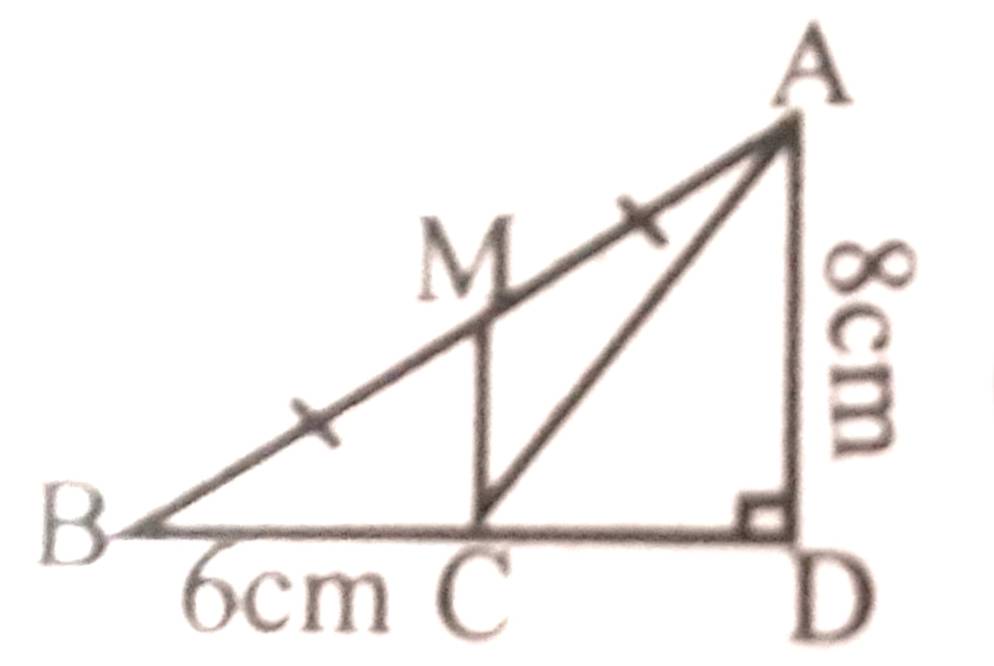
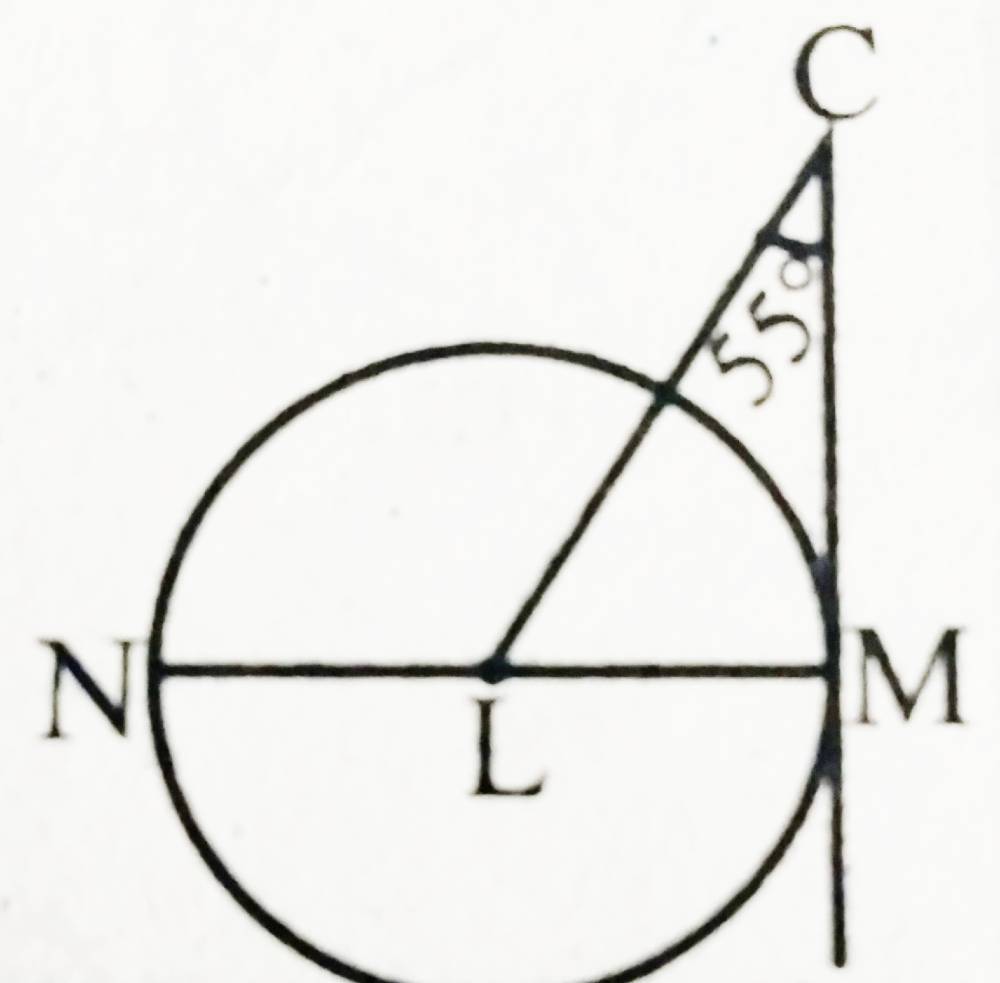
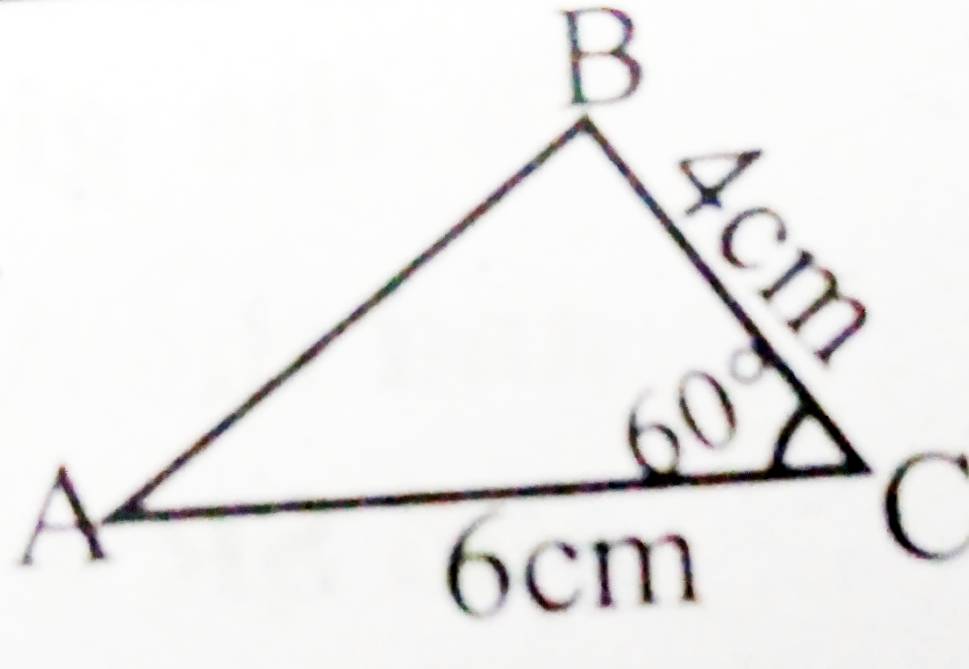
Quick Navigation
SEE Compulsory Math Question Paper With Solution
SEE 2077 (2021)
SEE Compulsory Math Model Set – 3
: 180 Mins
FM: 100
PM: 40
Group A - [ 3 x ( 1 + 1 ) = 6 ]
Group B - [ 4 x ( 2 + 2 ) + 3 x ( 2 + 2 + 2 ) = 34 ]
Group C - [ 10 x 4 = 40 ]
Group D - [ 4 x 5 = 20 ]
Popular Tags: 7 Days
Upcoming MCQs

Computer Fundamental Multiple Choice Questions Exam Free
- 2022-03-20 12:45
- 60 Mins
- 12 Enrolled
- 25 Full Marks
- 10 Pass Makrs
- 25 Questions