SEE Compulsory Math Question Paper With Solution
SEE 2077 (2021)
SEE Compulsory Mathematics Model Set – I
11
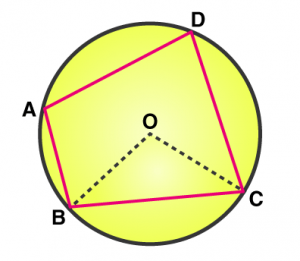
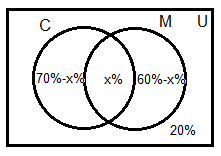
In a survey of people of a community, it was found that 70% liked curd, 60% liked milk, 20% don't like both curd and milk and 550 liked both curd and milk then,
- Draw a venn-diagram to illustrate above information
- Find total number of people participated in the survey
- Find the total number of people who liked curd only.
21
A person deposited Rs. 55,000 in bank 'p' for 2 years at 10% compound interest compounded annually. But after one year the bank changed the policy and decided to pay semi-annually, compound interest at the same rate. What is the percentage difference between the compound interest of the first and second year? Give reason with calculation.
22
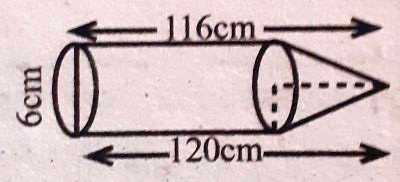
Two pillars of height 8 feet each with four faces shown of the gate of a stadium have one-one pyramid of height 4 feet each having same base on their tops. The base of each pillar is 6 ft x 6 ft. If the pillars with pyramid are painted at the rate of Rs. 75 per square feet, what will be the total cost?
Popular Tags: 7 Days
Upcoming MCQs

Computer Fundamental Multiple Choice Questions Exam Free
- 2022-03-20 12:45
- 60 Mins
- 12 Enrolled
- 25 Full Marks
- 10 Pass Makrs
- 25 Questions