Laws of transverse vibration of a string: Please refer to "State the laws of transverse vibration in a stretched string.".
Verification of the law of the transverse vibration:
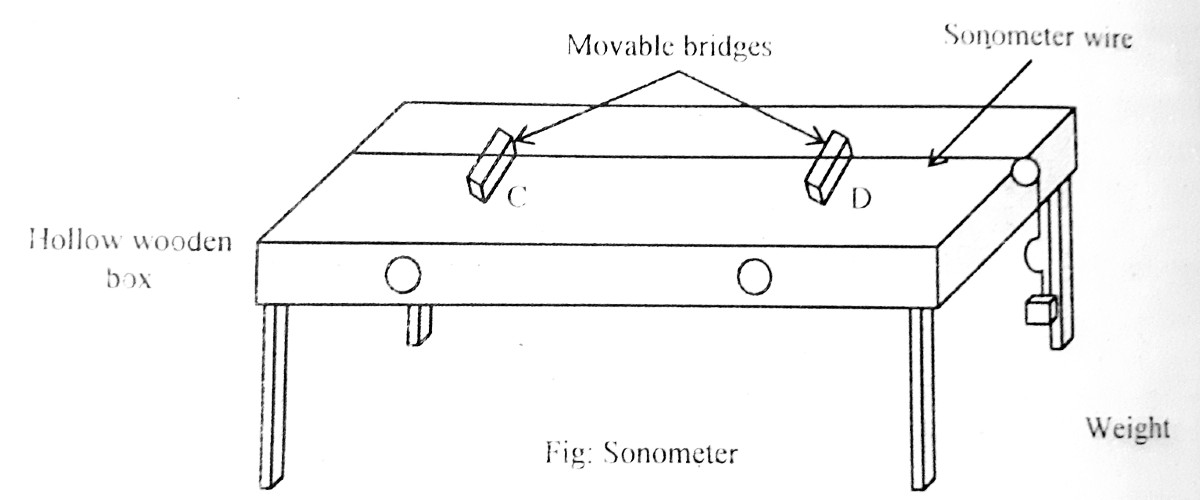
To verify the laws of vibration of a string, a sonometer is used. This device consists of a wire under tension which is arranged in a hollow wooden board as shown in Fig. The vibration of the wire is passed by a movable bridge to the box and then, to the air inside it.
- To verify f ∝ 1/l: To verify this law, take a tuning fork of known frequency. Taking a load of 1 kg on the string, find the resonating length of the wire between the bridges C and D. Let l1 be the resonating length for this tuning fork. The same process is repeated for the next tuning fork having a different frequency. Let l2 be the resonating length for the second tuning fork. It will be found that the product f1 x l1 = f2 x l2 at a constant tension and mass per unit length of the string. This follows that, \(f\propto\frac1l\)
- To verify f ∝ 1/√μ: To verify this law, the wires of different diameters and materials are used under the same vibrating length and the same tension. Taking a load of 1 kg on the string, find the resonating length of the wire between the bridges C and D. Let l be the resonating length for this tuning fork. Take another tuning fork of a different frequency and another wire of a different diameter. Taking a load of 1 kg on the string, find the resonating length of the wire between the bridges C and D. Now draw a graph between the frequency and 1/√μ, a straight line is obtained. this verifies that f\(f\propto\frac1{\sqrt\mu}\).