Laws of transverse vibration in a string:
The velocity of a transverse wave traveling in a stretched string is given by \(v=\sqrt{\frac T\mu}\), where T is the tension in the stretched string and μ is the mass per unit length. Since the frequency, f = v/2l in fundamental mode, then
\(f=\frac1{2l}\sqrt{\frac T\mu}\)
From the expression, it follows that there are three laws of transverse vibration of stretched string:
- The law of the length: The fundamental frequency is inversely proportional to the resonating length, l of the string.
\(f\propto\frac1l\)
- The law of the tension: The fundamental frequency is directly proportional to the square root of the stretching force or the tension.
\(f\propto\sqrt T\)
- The law of the mass: The fundamental frequency is inversely proportional to the square root of the mass per unit length.
\(f\propto\frac1{\sqrt\mu}\)
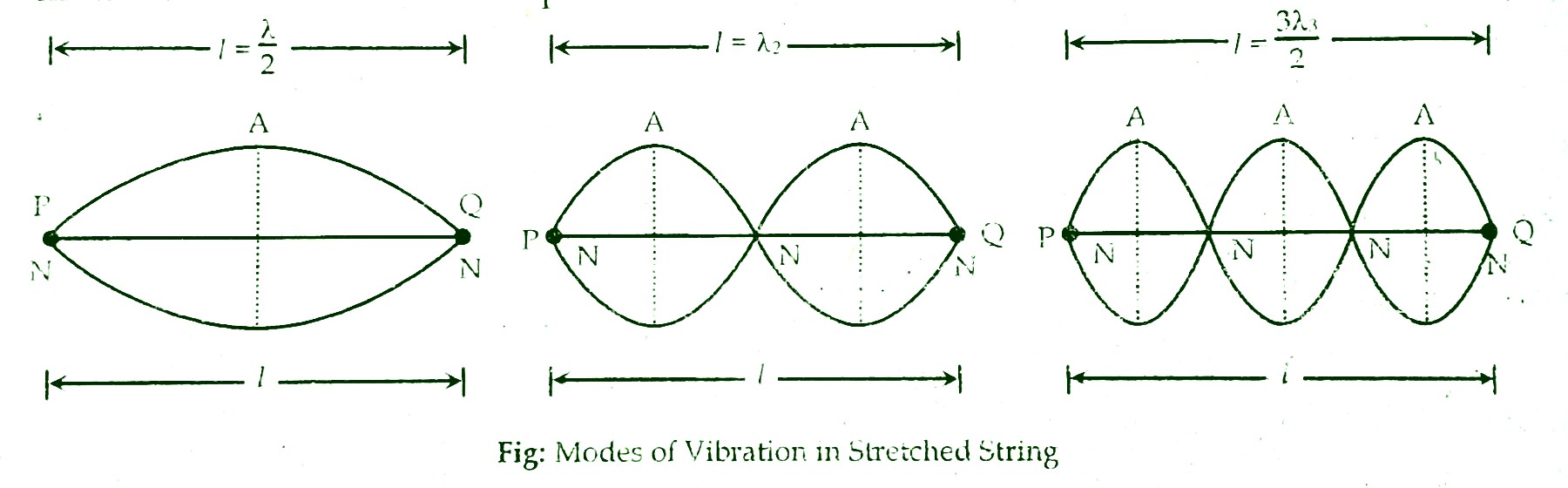
Modes of Vibration of a Stretched String
Let us consider a string that is stretched between two ends P and Q and plucked between these points produces a transverse wave. The stationary waves are thus set up in the string and the wire emits vibrations of different frequencies which are called modes of vibrations as shown in figures.
The First mode of vibration
Let a stretched string is plucked between two points P and Q in such a way that it forms only one segment. In this case, two nodes and one antinode are formed. If l be the length of string and λ1 be its wavelength, then the frequency is
\(f_1=\frac v{\lambda_1}=\frac v{2l}\)
Or, \(f_1=\frac1{2l}\sqrt{\frac T\mu}\)
This vibration is called fundamental mode or first harmonics and frequency is the fundamental frequency.
The Second mode of Vibration
Let a stretched string is plucked between the two points P and Q in such a way that it forms two segments. In this case, three nodes and two antinodes are formed. If l be the length of string and λ2 be its wavelength, then the frequency is
\(f_2=\frac v{\lambda_2}=\frac vl\)
Or, \(f_2=\frac12\sqrt{\frac T\mu}\) , \(\left[\because v=\sqrt{\frac T\mu}\right]\)
∴ f2 = 2f1
This vibration is called the second mode of vibration or second harmonics or the first overtone. The frequency in the mode is twice the frequency of fundamental frequency.
The Third mode of Vibration
Let a stretched string is plucked between two points P and Q in such a way that it forms three segments. In this case, four nodes and three antinodes are formed. If l be the length of string and λ3 be its wavelength, then its frequency is
\(f_3=\frac v{\lambda_3}=\frac{3v}{2l}\) , \(\left[\because\lambda_3=\frac{2l}3\right]\)
Or, \(f_3=\frac3{2l}\sqrt{\frac T\mu}\), \(\left[\because v=\sqrt{\frac T\mu}\right]\)
∴ f3 = 3f1
This vibration is called the third mode of vibration or the third harmonics or the second overtone. The frequency is three times the fundamental frequency. In general, for the nth mode of vibration, the frequency of vibration is fn = nf1 = f1 , 2f1 , 3f1 , ...., nf1