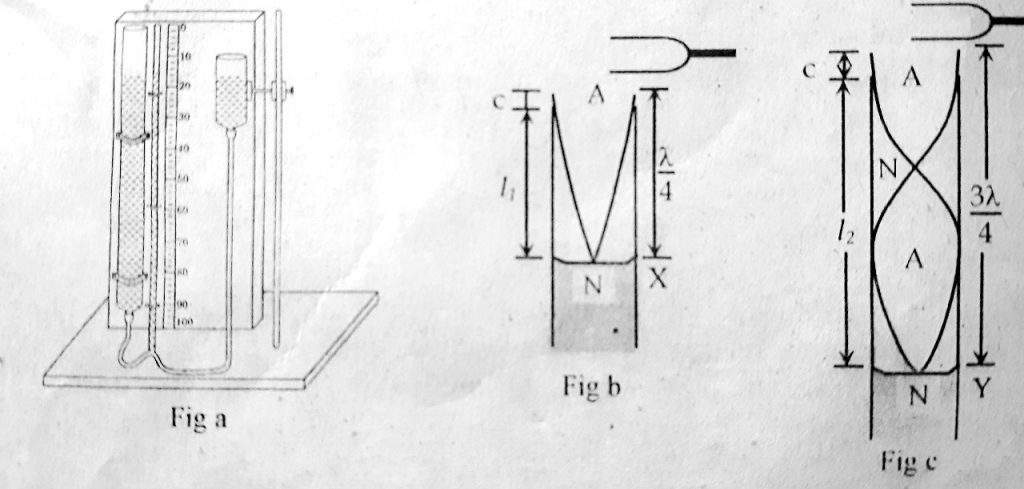
Measurement of the velocity of sound in air and end-correction of the tube (resonance tube experiment):
Resonance tube: It is a tube that is used to measure the velocity of sound in air, end correction of a tube, to compare the frequencies of the two given tuning forks. It consists of a metallic tube about 1m in length, about 3-5 cm in diameter whose upper end is open and the lower is closed with a large reservoir of water. The tube and reservoir are connected by a rubber tube. A meter scale is attached by the side of a tube which measures the length of the air column in the tube. The length of the air column is adjusted by raising or lowering the reservoir as shown in figure (a).
Working Principle: To find the velocity of sound in air, the water level in the tube is brought close to the open end of the tube by raising the reservoir. A sounding tuning fork is held horizontally at the surface and a stationary wave is formed as shown in figure (b), a sound is heard, the condition is called be the wavelength of the wave in the tube. So,
\(l_1+c=\frac\lambda2\) --------- (i)
Now, the water level is lowered further from position X until second resonance is again obtained and sound is heard at position Y as in figure (c). If l2 is the length of the air column for this second resonance, then,
\(l_2+c=\frac{3\lambda}4\) --------- (ii)
Subtracting equation (i) form (ii), we get,
\(l_2-l_1=\frac\lambda2\)
Or, \(\lambda=2\left(l_2-l_1\right)\)
Velocity of sound v = fλ = 2f(l2 - l1) -------- (iii)
Where, f is the frequency of the tuning form, knowing l1, l2 and f, v can be calculated at a giventemperature.
Substituting the valuye of \(\frac\lambda4\) from (i) and (ii), we get,
\(l_2+c=3(l_1+c)\)
Or, \(l_2+c=3l_1+3c\)
Or, \(2c=l_2-3l_1\)
∴ \(c=\frac{\displaystyle l_2-3l_1}2\) ---------- (iv)
Thus,knowing l1 and l2, c can be calculated using equation (iv)