The question is a bit unclear. So, I assume that the base of the pyramid is square. Here is the diagram according to the question.
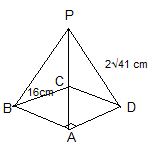
Consider the square base ABCD, and O the center of the square.
Here, length of diagonal BD = a√2 = 16√2 cm
∴ OD = BD / 2 = 8√2 cm
Now to find the height of the pyramid we consider right angles triangle POD. Using Pythagoras theorem, we get,
\(PO=\sqrt{PD^2-OD^2}\)
Or, \(PO=\sqrt{\left(2\sqrt{41}\right)^2-\left(8\sqrt2\right)^2}\)
Or, \(PO=\sqrt{4\times41-64\times2}\)
Or, \(PO=\sqrt{36}\)
Or, PO = 6 cm
Hence the height of the pyramid is 6cm
Now, volume of the pyramid is
V = \(\frac13\) x Base area x height
Or, \(V=\frac13BC^2\times PO\)
Or, \(V=\frac1316^2\times6\)
Or, \(V=256\times2\)
Or, V = 512 cm3
Hence the volume of given prism is 512 cm3 .





