Harmonics and overtones: All the modes of vibrations other than fundamental tones are called overtones. When the overtones have frequencies in exact multiples of the fundamental tone, they are called harmonics.
Organ Pipe: A hollow wooden or metallic tube used to produce sound is called an organ pipe. It is a wind instrument such as a flute, whistle, violin, clarinet, etc.
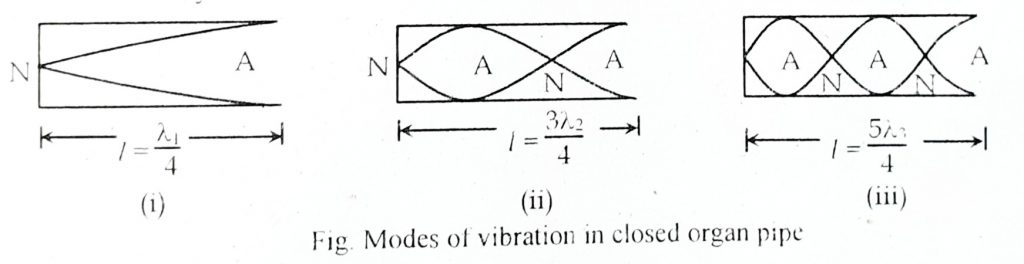
Wave in closed Pipe: The organ pipe which is closed to one end is called a closed organ pipe. Consider a closed organ pipe of length l as shown in the figure. A blast of air is blown into it at the open end and a wave thus travels, a stationary wave is produced. In the simplest mode of vibration, there is a displacement node, N at the closed end as the air is at rest and displacement antinodes, A at the open end as the air can vibrate freely. The different modes of vibration in closed organ pipe are given below.
Fundamental mode: In this mode of vibration, the pipe has one node at its closed end and one antinode at its open end. As observed in Fig. (i), the length, l of the pipe is equal to the distance between a node and an antinode which is λ1/4, where λ is the wavelength of the stationary wave. Then,
\(l=\frac{\lambda_1}4\)
or, \(\lambda_1=4l\)
If v is the velocity of sound and f1 is its frequency of vibration, then we have, v = λ1f1
Or, \(f_1=\frac v{\lambda_1}=\frac v{4l}\)
∴ \(f_1=\frac v{4l}\) ---------- (i)
It is the lowest frequency produced in the pipe. It is called fundamental frequency or the first harmonic.
The Second mode (The first overtone): In this mode of vibration, there are two antinodes and two nodes within the pipe as shown in Fig (ii). If λ2 is the wavelength of the wave, then we have
\(l=\frac{3\lambda_2}4\)
Or, \(\lambda_2=\frac{4l}3\)
The frequency of vibration, f2 is given by v = λ2f2
Or, \(f_2=\frac v{\lambda_2}=\frac v{4l/3}=\frac{3v}{4l}=3f_1\)
∴ f2 = 3f1 --------- (ii)
This is the frequency of the first overtone or the third harmonics.
The Third mode (The second overtone): In this mode of vibration, there are three nodes and three antinodes within the pipe as shown in Fig (iii). If λ3 is the wavelength of the wave, then
\(l=\frac{5\lambda_3}4\)
Or, \(\lambda_3=\frac{4l}5\)
If f3 is the frequency of the second overtone, then
v = λ3f3
Or, \(f_3=\frac v{\lambda_3}=\frac v{4l/5}=5\frac v{4l}=5f_1\)
∴ f3 = 5f1 ---------- (iii)
This is the frequency of the second overtone of the fifth harmonic.
Similarly, for the nth mode of vibration, the frequency of vibration is fn = (2n + 1)f1. In this way, other higher modes of vibration can be obtained. From equations (i), (ii), and (ii), it is observed that the frequency of higher modes of vibration is an odd integral multiple of the fundamental frequency f1. That is, f = f1, 3f1, 5f1, 7f1,.... only odd harmonics are present in the closed organ pipe.