Drift Velocity
In metal, there are some loosely bounded electrons. These types of electrons are called free electrons. They are in a random motion like the gas molecules contained in a container. These free electrons are randomly distributed in all directions. But when an electric field is applied in the conductor, the electrons keep colliding with atoms with gaining and losing their kinetic energy. However, they acquire an average velocity opposite to the direction of the applied field. The average velocity of free electrons with which they drift in the direction opposite to the field is called drift velocity. Thus, the average velocity of charge carriers (electrons) with which they move in a conductor under the influence of an applied electric field is called drift velocity. it is denoted by Vd
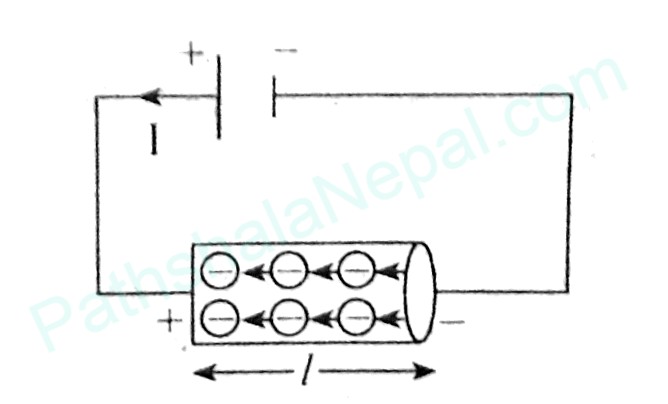
Let us consider a metallic conductor, cylindrical in shape, with cross-sectional area A and length l. If n be the number of electrons per unit volume and e bt the charge of each electron.
Total free charge in volume V is, (Q) = volume of conductor x total number of electrons x electric charge
∴ Q = Alne [ because V = A x l ]
Let 'I' be the current flowing through the conductor, the free electrons drift in the direction opposite to the direction of the applied field electric field is as shown in the figure. Let vd be the drift velocity of the free electrons. If t be the time required to drift total charge through length l, then-current is given by
\(I=\frac Qt=\frac{neAl}t\)
Or, \(I=neA\frac lt\)
Or, \(I=neAv_d\)
\(\Rightarrow I=v_denA\)
Or, \(v_d=\frac I{neA}\)
This equation gives the expression for drift velocity. Further, the current flowing per unit cross-sectional area is called current density. it is denoted by I and is given by,
\(J=\frac IA=\frac{v_denA}A\)
\(\Rightarrow J=nev_d\)
Since, \(\overrightarrow j\) and \(\overrightarrow{v_d}\) are vector quantities, so \(\overrightarrow j=ne\overrightarrow{v_d}\), which is the required expression of current density.