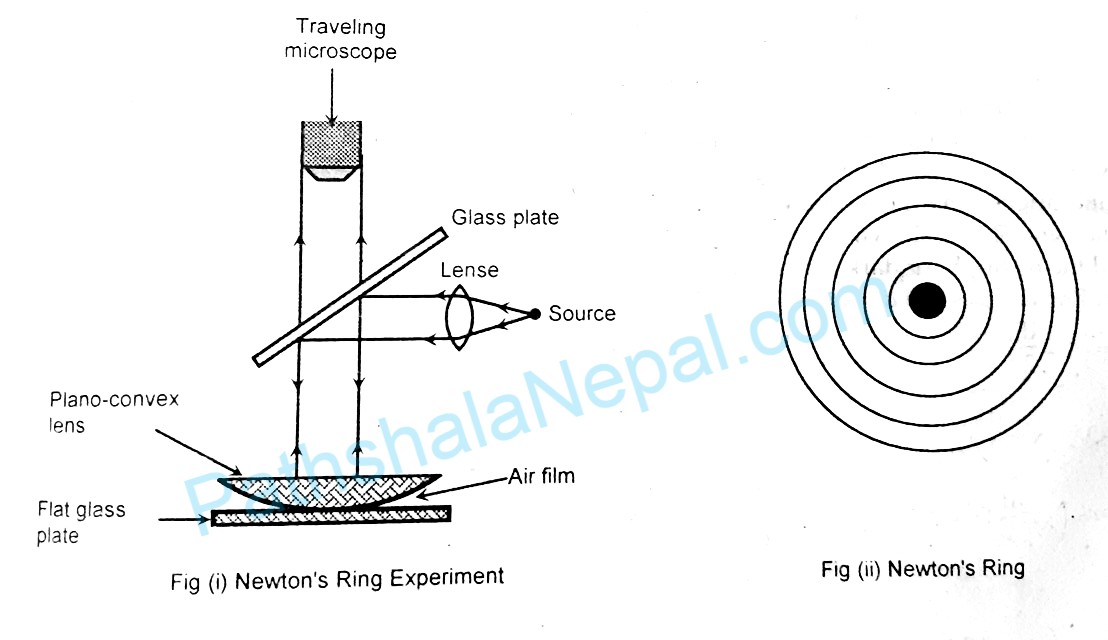
Newton's ring experiment (Determination of Wavelength of Light)

Newton’s Ring Experiment apparatus for determination of the wavelength of the light consists of a plano-convex lens placed on a flat glass plate, a source of light (generally sodium light), a glass plate kept at 45° to the incident beam, and a traveling microscope. The apparatuses are arranged as shown in the figure. A source of light S is plated at the focus of the convex lens. The ray of light after passing through this lens becomes parallel and strikes the glass plate which is partially silvered. These rays get reflected and strike the plano-convex lens. The air film is formed between the flat glass plate and the lower face of the plano-convex lens. The air film is formed circular and width varies from zero to infinity. The light rays reflected from the upper surface of glass plate and lower surface of the plano-convex lens has some path difference. These reflected rays get superimpose and form an interference pattern in the form of a ring called Newton’s ring. The central ring is dark and then alternate dark and bright rings are formed as shown in the figure. These rings are formed due to the superposition of the reflected beam of light. Here the radius of the n^th bright ring is \(r_n=\sqrt{\left(\frac{2n-1}n\right)\lambda R}\) and the n^th dark ring is r_n \(r_n=\sqrt{n\lambda R}\) where λ is the wavelength of light and R is the radius of the plano-convex lens.

Determination of Wavelength of Light:

If D_n be the diameter of n^th dark fringe, then \(r_n=\frac{D_n}2\)

∴ \(\frac{D_n}2=\sqrt{n\lambda R}\)

Or, \(D_n^2=4n\lambda R\)

Similarly, If \(D_{m+n}\) be the diameter \(\left(m+n\right)^{th}\) dark ring, then we can write.

\({D^2}_{m+n}=4(m+n)\lambda R\)
Or, \({D^2}_{m+n}-{D^2}_n=4m\lambda R\)
Or, \(\lambda=\frac{{D^2}_{m+n}-{D^2}_n}{4mR}\)

From this formula, we can calculate the wavelength of light by using Newton's Ring.